刷题笔记-二叉树

C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn
unordered_map、unordered_map底层实现是哈希表
顺序存储完全二叉树: 如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2
深度优先遍历(前中后序)一般通过递归实现, 也可通过栈使用非递归实现
广度优先遍历(层次遍历)一般通过队列实现

二叉树创建

public TreeNode CreateTree(Integer[] c) {
    if (size >= c.length) {
        return null;
    }
    Integer var = c[size++];
    if (var == null) {
        return null;
    }
    TreeNode node = new TreeNode(var);
    System.out.println(var);
    node.left = CreateTree(c);
    node.right = CreateTree(c);
    return node;
}

深度优先遍历(递归)

前序

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        ArrayList<Integer> res = new ArrayList<>();
        traversal(root,res);
        return res;
    }
    void traversal(TreeNode cur,List<Integer> res){
        if(cur==null){
            return;
        }
        res.add(cur.val);
        traversal(cur.left,res);
        traversal(cur.right,res);
    }
}

中序

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        ArrayList<Integer> res = new ArrayList<>();
        traversal(root,res);
        return res;
    }
    void traversal(TreeNode cur,List<Integer> res){
        if(cur==null){
            return;
        }
        traversal(cur.left,res);
        res.add(cur.val);
        traversal(cur.right,res);
    }
}

后序

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        ArrayList<Integer> res = new ArrayList<>();
        traversal(root,res);
        return res;
    }
    void traversal(TreeNode cur,List<Integer> res){
        if(cur==null){
            return;
        }
        traversal(cur.left,res);
        traversal(cur.right,res);
        res.add(cur.val);

    }
}

深度优先遍历(非递归, 利用栈)

前序

较为简单, 因为对每一个节点的孩子来说, 他都是根节点, 在访问到它时, 直接将他的值放入数组

public List<Integer> preorderTraversal(TreeNode root) {
    ArrayList<Integer> result = new ArrayList<>();
    if (root == null) {
        return result;
    }
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        result.add(node.val);
        if (node.right != null) {
            stack.push(node.right);
        }
        if (node.left != null) {
            stack.push(node.left);
        }
    }
    return result;

}

中序

较前序复杂, 因为访问到一个节点时, 需先放入栈中, 直到它的左子树为空, 才弹出将它的值放入数组

public List<Integer> inorderTraversal(TreeNode root) {
    ArrayList<Integer> result = new ArrayList<>();
    if (root == null) {
        return result;
    }
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    while (cur != null || !stack.isEmpty()) {
        if (cur != null) {
            stack.push(cur);
            cur = cur.left;
        } else {
            cur = stack.pop();
            result.add(cur.val);
            cur = cur.right;
        }
    }
    return result;

}

后序

利用一个规律–根右左的遍历结果反转一下就是后序遍历结果

为什么这样做呢, 因为这样跟前序一样简单

public List<Integer> postorderTraversal(TreeNode root) {
    ArrayList<Integer> result = new ArrayList<>();
    if (root == null) {
        return result;
    }
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        result.add(node.val);
        if (node.left != null) {
            stack.push(node.left);
        }
        if (node.right != null) {
            stack.push(node.right);
        }
    }
    Collections.reverse(result);
    return result;
}

深度优先遍历一致性代码(非递归)

public List<Integer> postorderTraversal(TreeNode root) {
  ArrayList<Integer> result = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
  if (root != null) {
      stack.push(root);
  }
  TreeNode node = null;
  while (!stack.isEmpty()) {
           node = stack.peek();
      if (node != null) {
          stack.pop();
          // 后序遍历
          stack.push(node);
          stack.push(null);
          if (node.right != null) {
              stack.push(node.right);
          }
          if (node.left != null) {
              stack.push(node.left);
          }
          // 后序遍历 从下向上看, 左右根, 为后序
      } else {
          stack.pop();
          node = stack.pop();
          result.add(node.val);
      }
  }
  return result;
}

其他遍历顺序只需调整一下注释部分的顺序

广度优先遍历

public List<List<Integer>> levelOrder(TreeNode root) {
    List<List<Integer>> resList = new ArrayList<List<Integer>>();
    if (root == null) {
        return resList;
    }
    Queue<TreeNode> que = new LinkedList<TreeNode>();
    que.offer(root);
    while (!que.isEmpty()) {
        int len = que.size();
        ArrayList<Integer> al = new ArrayList<Integer>();
        while (len > 0) {
            TreeNode node = que.poll();
            al.add(node.val);
            if (node.left != null) {
                que.offer(node.left);
            }
            if (node.right != null) {
                que.offer(node.right);
            }
            len--;
        }
        resList.add(al);
    }
    return resList;
}

广度优先遍历(返回一维数组, 如果节点没有左孩子或右孩子, 为null)

public ArrayList<Integer> levelOrder(TreeNode root) {
    ArrayList<Integer> resList = new ArrayList<>();
    if (root == null) {
        return resList;
    }
    Queue<TreeNode> que = new LinkedList<TreeNode>();
    que.offer(root);
    while (!que.isEmpty()) {
        boolean flagR = false;
        TreeNode node = que.poll();
        resList.add(node.val);
        if (flagR) resList.add(null);
        if (node.left != null && node.right != null) {
            que.offer(node.left);
            que.offer(node.right);
        }
        if (node.left != null && node.right == null) {
            que.offer(node.left);
            flagR = true;
        }
        if (node.left == null && node.right != null) {
            resList.add(null);
            que.offer(node.right);
        }
        if (node.left == null && node.right == null) {
            resList.add(null);
            resList.add(null);
        }
    }
    return resList;
}

from collections import deque
class Solution:
    def levelOrder(self, root: TreeNode) -> List[int]:
        if not root:
            return [1]
        res=[]
        l=deque()
        l.append(root)
        
        while len(l)!=0:
            root=l.popleft()
            res.append(root.val)
            if root.left:
                l.append(root.left)
            else:
                res.append(None)
            if root.right:
                l.append(root.right)
            else:
                res.append(None)
        return res



t=TreeNode(3)
t.left=TreeNode(9)
t.right=TreeNode(20)
t.right.left=TreeNode(15)
t.right.right=TreeNode(7)
s = Solution()
s.levelOrder(t)

貌似和上边的Java代码效果一样…

最底层最左边节点的值

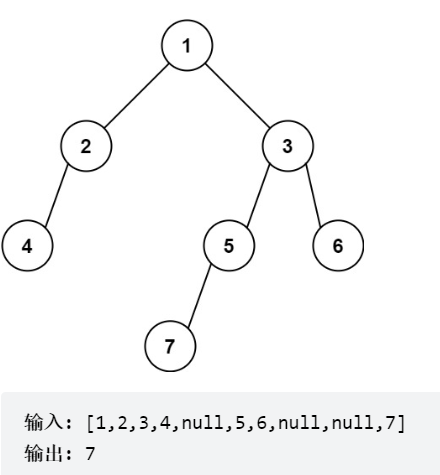
public int findBottomLeftValue(TreeNode root) {
      Queue<TreeNode> queue = new LinkedList<>();
      queue.offer(root);
      while(!queue.isEmpty()){
          root = queue.poll();
          if (root.right != null) queue.offer(root.right);
          if (root.left != null) queue.offer(root.left);
      }
      return root.val;
  }

队列广度遍历，先放右孩子，保证最后出来是最左

int max = Integer.MIN_VALUE;
int res;
public int findBottomLeftValue(TreeNode root) {
    dfs(root, 0);
    return res;
}
public void dfs(TreeNode node, int depth){
    if(node != null){
        if(node.left == null && node.right == null){
            if(max < depth){
                max = depth;
                res = node.val;
            }
        }
        dfs(node.left, depth + 1);
        dfs(node.right, depth + 1);
    }
}

深度搜索＋递归, 一条路行到黑, 只要不是叶子节点, 就递归左右, 碰到叶子节点再比较深度, 由于同一层次最左边的值先赋值给res, 右边深度相等, 不会赋值.

刷题笔记-二叉树

二叉树创建

深度优先遍历(递归)

深度优先遍历(非递归, 利用栈)

深度优先遍历一致性代码(非递归)

广度优先遍历

广度优先遍历(返回一维数组, 如果节点没有左孩子或右孩子, 为null)

最底层 最左边 节点的值

最底层最左边节点的值